Of the four sections of the ACT, the Math section tests the widest variety of topics. It’s also the only section with a set order of difficulty, with the hardest questions coming towards the end of the section. Consequently, many students feel intimidated by the latter part of the Math section and struggle to identify any unifying strategies. Of the varying math topics, geometry is especially difficult due to the wide array of possible questions types. Nevertheless, by applying a few general techniques, students can greatly simplify the hardest geometry problems.
The techniques in the article will ensure that the a-ha moment happens during, not after, the test.
The first step in solving any problem is identifying it. Students who tend to benefit most from the techniques outlined in this article are high-scoring math students who sometimes find themselves unsure of how to initially proceed on geometry problems from the second half of the Math section. Implementing the following strategies will help these students turn murky problems into clear ones with actionable steps. The other type of student who will find these strategies useful is the “a-ha” student—i.e. the student who constantly finds herself saying “I knew that!” when her tutor shows her an answer to a problem. The techniques in the article will ensure that the a-ha moment happens during, not after, the test.
The most basic technique that students should use on difficult geometry problems is to underline what the question is asking for and identify relevant equations. Unlike the SAT, the ACT does not provide students with a list of geometry equations and theorems. It is therefore vital that students memorize all of the most commonly used equations for circles, triangles, and quadrilaterals. Once a student identifies the pertinent equation for a particular question, the step-by-step process for solving the problem becomes much clearer. Let’s take a look at a sample problem the see this in action:
The figure below shows a circle inscribed in a square. If the area of the circle is 25π , what is the area of the square?

- What is the question asking for? The area of the square.
- What are the equations associated with this? A = s² (i.e. We need to find the side length.)
- Are there other pieces of information associated with equations? Yes, Acircle = πr²
- Start with given information + equations and solve. 25π = πr², r = 5
The next step is to add new information to the figure in a useful way. We just found that the radius is 5. How can we add that information to the figure in a way that helps us find what we identified in steps 1 and 2? In this problem, successfully adding r = 5 to the figure will help us identify the side length of the square. Generally, you should look to connect multiple shapes.
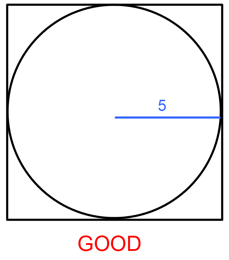
The second figure makes it clear that the side length of the square is twice the radius. Therefore, s = 10. Using the equation we found in step 2, A = s² = 10² = 100.
Geometry questions from the second half of the ACT Math section can seem confusing and difficult. To score well on these questions, it is imperative that a student know all of the geometric equations and theorems. With that knowledge, a student can follow the techniques outlined in this article to identify the small steps that are necessary to solve the most difficult problems.
Related Posts
How To: Answer Trigonometry Questions
How To: Substitute Numbers for Variables





