One of the more unique traits of the ACT Math section is the high frequency of relatively straightforward math problems that are disguised in potentially tricky language. These can come either in the form of traditional word problems or in the form of technical-sounding sentences that describe what a particular math equation should be. There are a number of reasons that a student might find these questions difficult; in my experience as a tutor, however, these questions are especially difficult for students whose math instruction has predominately been in a language other than English. If you fall into that category, or if you frequently find yourself getting stuck on wordy Math questions only to realize later that the question wasn’t really an advanced one, I think you’ll find this article helpful.
The first observation I’d like to make is that math is its own language. Instead of words, we have numbers, and instead of punctuation such as periods and commas, we have symbols such as “+” and “÷”. If you were learning a new language—let’s say, French—and you wanted to translate Le Pettit Prince into English, what would you need? A French-English dictionary, of course. Similarly, we will build our own “Math-English” dictionary to help us translate wordy ACT questions into simple math equations. I’m going to use two examples to illustrate the process of how to build this dictionary before giving you the most common terms that you’ll need to use.
The most consistently tricky word to translate from English to math is “of”. When I ask my students what they think “of” means, most say “division.” This makes a lot of sense, and this is the same answer that I gave my Algebra II teacher when she asked me this question way back in… well, let’s not talk about when I went to high school! Equating “of” with division is intuitive because when we think of division, we think of fractions, and when we think of fractions, we think “a part of something.” In order to double check myself, however, I like to give myself extremely simple questions to see if I’m translating English to math properly. What’s half of 8? What’s one-third of 18? What is three-fourths of 20? As you answer “four”, “six”, and “fifteen” to these questions, it becomes clear that the math operation that you are doing in your head is not division but multiplication. On the ACT Math section, when you see “of,” think “multiplication.”
Another phrase that many students struggle with is “less than.” This one seems as if it should be easy. Surely “less than” means “subtraction,” right? While this is true, the problem here lies not in which operation to choose but in what order to subtract. If I ask a student to represent “two less than x” as a math expression, I usually get “2 minus x” as an answer, which is exactly what you would get if you substituted “minus” for “less than.” But as we did in the previous example, let’s put this theory to the test with a simple question. What is 3 less than 14? Well, using the straightforward method of substituting “minus” for “less than,” we would have “3 minus 14,” which is a negative number. It’s clear that “3 less than 14” should give us 11, however, and this leads us to our second entry in the Math-English dictionary: when substituting “minus” for “less than,” make sure to switch the order of the numbers or variables being subtracted.
The ArborBridge curriculum includes several lessons devoted to the language of mathematics, and we’ve identified dozens of words and phrases as well as their symbolic counterparts. I’ll give you the most common ones here, and even if you only memorize these, you should find yourself approaching these problems in a much more effective way.
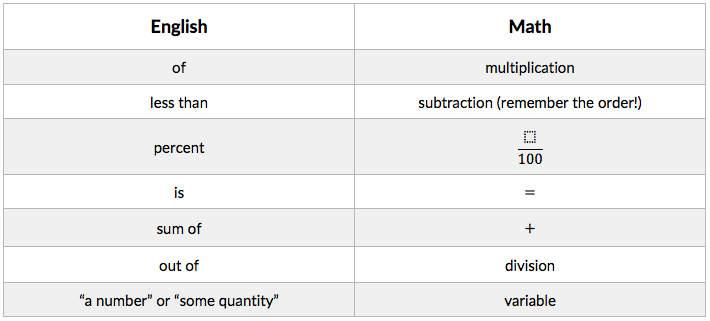
Finally, let’s look at an example of an ACT Math problem and see how we can translate it into a math equation.
1. Seven less than a number is 15% of twice that number. What is the number?
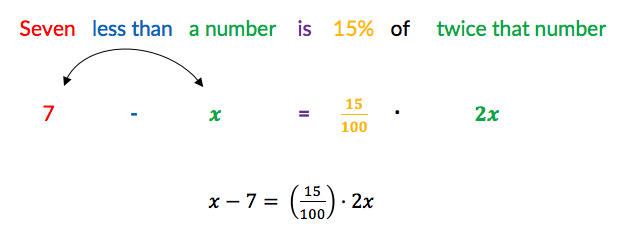
By using our math-English equivalencies, we've turned a complicated sounding sentence into an equation that is straightforward and easy to solve.
Related Posts
How To: Understand American Measurements
How To: Substitute Numbers for Variables





