Today, let’s talk about an issue that impacts every student and can occur on any question type: careless errors. At one point in time, we’ve all reviewed some of our own work and thought, “how did I make such a stupid mistake?” While it’s easy to view these careless errors as annoying-but-inevitable, there are certain techniques that you can employ to minimize these mistakes on the ACT Math section.
First, I’d like to stress the importance of minimizing errors. The Math section is the only part of the ACT that increases in difficulty as you progress through it, but that doesn’t mean that the later questions are any more important than the earlier ones. Every question is worth the same number of points, and if you can avoid a careless error early in the section, it has the same impact on your score as getting a very difficult question correct.
One of the best ways of minimizing careless errors is to simply take a few seconds to review your answer after you’re done with the problem. I suggest that you ask yourself two questions after each math problem. Number one: Did I answer the question that was asked? This might seem trivial, but I can tell you that in my experience as a tutor, the most frequent careless error that students make is answering a question other than the one they are asked. Sometimes they solve for the wrong variable, sometimes they solve for radius when they are asked for circumference, sometimes they forget to convert to the proper units, etc. Whatever the situation, it is worthwhile to double-check that your response actually answers the question.
The second question you should ask yourself is: Did I overlook any important information? On the Math section, you need to make use of every piece of information you are given in a problem. If you didn’t use something that was given to you, your answer is likely incorrect.
Now, let’s move to some examples of common careless errors that students frequently make on the Math section. Probably the most frequent mistake that I see involves not distributing during multiplication properly. Let’s look at two examples:
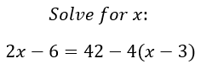
Here, it’s very common to make the following mistake:
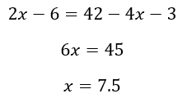
When distributing a negative number into a set of parentheses, make sure that you distribute it onto all terms inside of the parentheses. Like this:
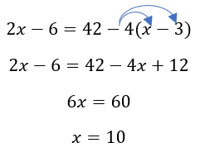
One way to check for this type of error is to take your answer and plug it back in to the original equation. If it doesn’t work, you made a mistake.
Another common careless mistake relates to squares and square roots. I see even advanced students making these two mistakes. Remember:
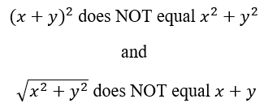
Finally, a third common mistake stems from the way that the ACT words some of its questions. Again, let’s learn by looking at an example:
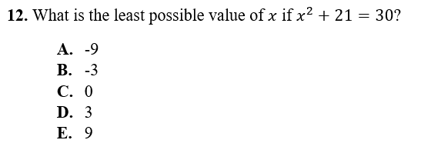
The “quick way” to do this problem is to subtract 21 from both sides, take the square root, and get x = 3. But remember that if x2 = 9, then x equals three or negative three. On questions asking you for the largest or smallest possible value, be aware that multiple given answers may fit the equation, but only one answer meets all the criteria stated in the question.
I hope this gives you some informative examples of common careless errors and some techniques for avoiding them. Remember that every question counts: if you slow down and work deliberately, you will avoid losing points on material you know.
Related Posts
How To: Substitute Numbers for Variables
How To: Translate Wordy Problems from English to Math





